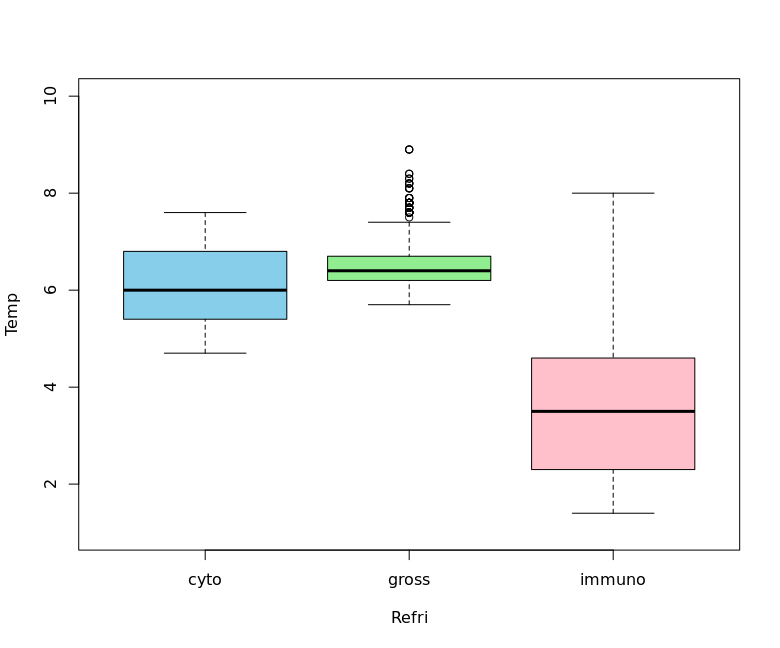
gross 항목의 whisker를 구해보도록 하자. boxplot의 위쪽 whisker는 (Q3-Q1) * 1.5 를 넘어서는 값으로 알려져 있다.

Box plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying statistical distribution[3] (though Tukey’s boxplot assumes symmetry for the whiskers and normality for their length). The spacings in each subsection of the box-plot indicate the degree of dispersion (spread) and skewness of the data, which are usually described using the five-number summary. In addition, the box-plot allows one to visually estimate various L-estimators, notably the interquartile range, midhinge, range, mid-range, and trimean. Box plots can be drawn either horizontally or vertically.
boxplot.stats() 을 이용하면 구할 수 있다. dataframe이나 list 형식의 자료는 처리할 수 없다. pull()을 이용해서 자료를 추출한다.
> boxplot.stats(dt %>% filter(Refri == 'gross') %>% pull(Temp))$stats
[1] 5.7 6.2 6.4 6.7 7.4
$n
[1] 1647
$conf
[1] 6.380534 6.419466
$out
[1] 8.9 8.9 8.4 8.4 8.2 7.8 7.6 7.6 7.6 7.6 7.7 7.8 7.8 7.8 8.1 7.8 7.7 7.8 7.8 8.1 7.6 7.8 7.7 7.6 7.9 7.8 7.8 7.7 7.6 7.9 8.1 8.3 7.8 8.2 7.6 7.8 7.7 7.9 7.5 7.7 7.8 7.7 7.6 7.8 7.8
[46] 8.1 8.2 7.6 7.8 7.6 7.6 8.9 8.2 8.3 7.6 7.9 7.6그러면 $out 항목에서 whisker 값을 알 수 있다.
사용할 때 주의할 점. 이렇게 구한 것은 coef = 1.5가 기본값이다. 통계의 주요 5값을 구하려면 coef = 0을 지정해야 한다.
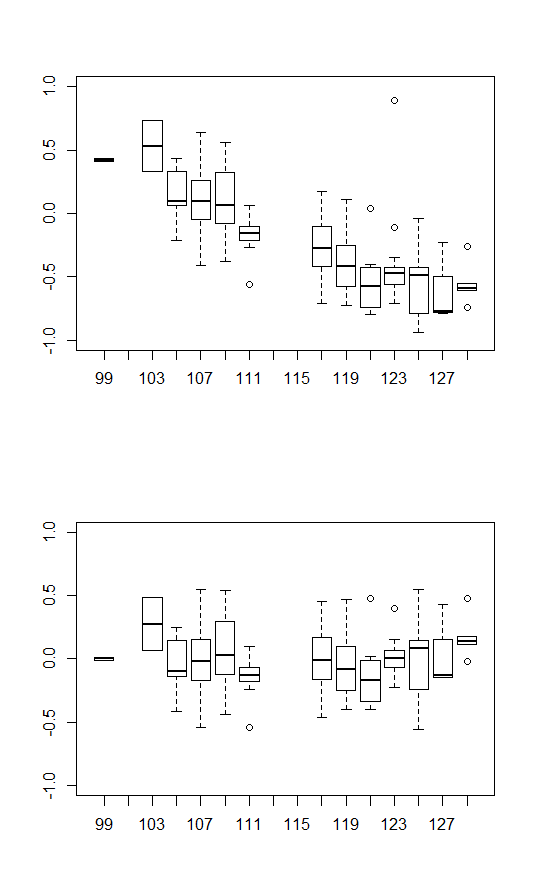


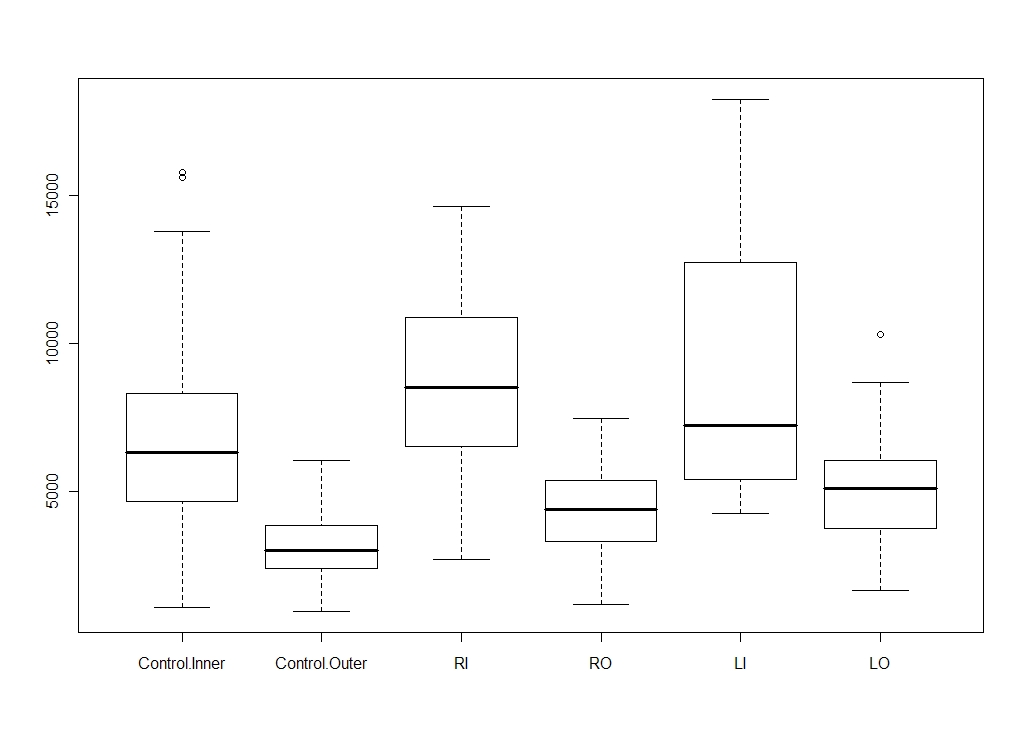
 Case report 준비하면서 통계 프로그램인 R을 사용하여 Boxplot 을 만들어 보았다. 그래프상 이 자료는 전혀 도움이 안될 것 같다. 미묘하게 측정값이 커졌다는 것을 알지만 충분히 오래동안(??) 살지 못한 상태에서 보상작용이 충분하게 일어나지 않아서 그런지는 몰라도 좀 크기가 작은 것 같다.
Case report 준비하면서 통계 프로그램인 R을 사용하여 Boxplot 을 만들어 보았다. 그래프상 이 자료는 전혀 도움이 안될 것 같다. 미묘하게 측정값이 커졌다는 것을 알지만 충분히 오래동안(??) 살지 못한 상태에서 보상작용이 충분하게 일어나지 않아서 그런지는 몰라도 좀 크기가 작은 것 같다.