Author: byun1114

남한 정도의 지형에서라면 굳이 구면 혹은 타원체 두 점 사이의 거리를 이용해야 할 정도는 아닐 것이다. 그럼에도 불구하고 처리 시간이 엄청 바뀌지 않는다면 제대로 측정해 보는 것도 좋을 것이다.

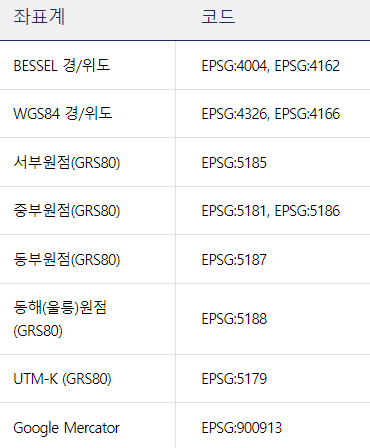
좌표계 변환에 사용했던 pyproj 의 Geod 를 이용한다. 입력값으로 scalar와 array 모두 가능하다. 그렇다면 편리하게 array 형식으로 한 번에 계산한다.

geo = pandas.read_csv("area_data.csv")

import pyproj
g = pyproj.Geod(ellps='WGS84')
_,_,dist = g.inv([target_long] * len(geo), 
                 [target_lati] * len(geo), 
                 geo['longitude'],
                 geo['latitude'])
geo['distance'] = dist
geo.sort_values(by='distance', inplace = True)

결과적으로 보면 이렇게 할 경우 거리는 m 단위로 나오는 것 같다.

GPS로 얻을 수 있는 좌표는 WGS84 좌표계이다. 다른 표현으로 EPSG:4326이다.

기상청 예보는 좌표계로 도로명 주소를 이용한다. 초단기예보는 동네까지 적용된다. 기술문서에 주소와 GPS 좌표가 있는 엑셀 파일을 제공한다. 이를 이용하여 현재 GPS 좌표와 가장 가까운 대표 주소를 알아낼 수 있다.

에어코리아에서는 TM 좌표를 이용한다. TM이라는 것은 표현 방식에 대한 것으로 어떤 좌표계를 말하는 것인지 알 수 없다. 정부기관에서 하는 일이니까 적어도 표준적인 좌표계를 쓸 것 같았다. 인터넷 검색으로 통계청 자료 자료를 구할 수 있었다.

기술 문서에 ‘중부원점’ 표현이 있다. 따라서, EPSG:5181과 EPSG:5186 중 하나일 가능성이 높다.

이런 예시의 진위 여부가 고민이기는 한데, 소수점 이하까지 만들어 내는 것은 쉽지 않을 것이다. 이 예시를 참고한 결과 EPSG:5181 좌표계를 이용한 것 같다.

EPSG:4326의 좌표를 EPSG:5181로 변환하려면 다음과 같이 한다. 이 함수를 이용할 때 X와 Y 순서가 반대로 되어 있음에 유의하자.

import pyproj
y, x = pyproj.Transformer.from_crs("epsg:4326", "epsg:5181").transform(target_lati, target_long)

Jupyterlab 환경에서는 커널을 종료하기 전까지 이전 변수가 저장되어 있다. 이전 변수가 남아 있어 프로그램이 올바르게 실행되지 않는 경우가 있다. Bing 에서 검색하니 다음의 코드를 알려 주었다.

import sys
for var in list(globals()):
    if var not in ['__name__', '__doc__', '__package__', '__loader__', '__spec__', '__annotations__', '__builtins__']:
        del globals()[var]